利用质中心能量为\(\sqrt{s}=13\) TeV的质子-质子碰撞数据,给出了射流能量尺度的确定方法,该数据对应于在大型强子对撞机上使用ATLAS探测器收集的140 fb\(^{-1}\)的综合光度。利用ATLAS粒子流方法重建射流,该方法结合了带电粒子轨迹和由热量计电池中的能量沉积形成的拓扑簇。采用半径参数为\(R=0.4\)的反(k_ extrm{t}\)射流算法来定义射流。本文报道了为LHC第2次运行开发的新型射流能量尺度标定策略,为第3次运行的射流标定奠定了基础。喷气机通过一系列基于模拟的校正进行校准,包括最先进的喷气机校准技术,如机器学习方法和新颖的原位校准,以获得比使用高达81 fb\(^{-1}\) Run 2数据导出的基线校准更好的性能。这些新技术的性能,然后通过利用射流和参考物体之间的横向动量平衡在原位测量中进行检验。使用粒子流射流的b-夸克射流能量尺度首次使用\(\gamma \)+射流事件以约1%的精度测量。
大型强子对撞机(LHC)产生的高能质子-质子(pp)碰撞产生的最终状态主要以喷流为特征,喷流是带电和中性强子及其衰变产物的准直喷雾。射流构成了使用ATLAS探测器进行的物理项目的重要组成部分,对射流重建的精确理解对于各种各样的过程至关重要。因此,测量这些复杂天体的射流能量尺度(JES)和分辨率(JER)对于精确测量标准模型和寻找超越标准模型的新现象至关重要。提出了几种改进射流能量标度校准的新方法,并对其在仿真和数据中的性能进行了评估,为JES在Run 3及以后实现更高的精度铺平了道路。这些技术是针对使用粒子流输入[3,4],采用半径参数的反算法[1,2]重建射流而开发的。ATLAS协作组织以前的校准策略使用了多达81 fb的数据[4,5,6,7,8,9],通过利用140 fb的完整Run 2数据样本进行了扩展和改进。
射流能量标度标定包括一系列标定步骤。校准的第一阶段使用模拟来获得射流能量尺度的修正,以减少堆积、探测器效应和其他参数的影响。校准的第二阶段是残余原位校准,校正数据和蒙特卡罗(MC)模拟之间的剩余差异,使用测量良好的参考物体,包括光子和Z玻色子。
本文的结构如下。第2节描述了ATLAS探测器,第3节描述了记录的数据和MC模拟样本,以及用于重建射流的输入和算法。第4节描述了基于模拟的校准的方法和结果,第5节描述了原位校准,第6节给出了结论。
大型强子对撞机的ATLAS探测器[10]几乎覆盖了碰撞点周围的整个立体角。它由一个内部跟踪探测器组成,周围是一个超薄超导螺线管,电磁和强子量热计,以及一个包含三个大型超导空芯环形磁体的μ子光谱仪。
内部探测器系统(ID)浸泡在2t轴向磁场中,并在范围内提供带电粒子跟踪。高粒度硅像素检测器覆盖顶点区域,通常每个轨道提供四次测量,第一次命中通常在运行2之前安装的可插入b层(IBL)中[11,12]。其次是硅微带跟踪器(SCT),通常每个磁道提供8个测量值。这些硅探测器由过渡辐射跟踪器(TRT)补充,它可以实现径向扩展的轨道重建。TRT还提供电子识别信息,该信息是基于高于与跃迁辐射对应的较高能量沉积阈值的命中比例。
该量热计系统的伪快度范围为。在该地区,电磁量热由桶状和端盖式高粒度铅/液氩(LAr)量热计提供,并带有额外的薄LAr预采样器覆盖,以纠正量热计上游材料的能量损失。强子量热计由钢制/闪烁体-瓦式量热计提供,分为三个桶状结构内部和两个铜/LAr强子端盖量热计。立体角覆盖由分别针对电磁和强子能量测量优化的正向铜/LAr和钨/LAr量热计模块完成。
μ子谱仪(MS)由单独的触发室和高精度跟踪室组成,用于测量超导空芯环形磁体产生的磁场中μ子的偏转。环面在探测器大部分区域的场积分在2.0 ~ 6.0 T m之间。覆盖该区域的三层精密腔室,每层由监测漂移管层组成,在背景最高的前方区域配有阴极带腔室。该介子触发系统覆盖了筒体内的阻板室和端盖区域的薄间隙室的范围。
感兴趣的事件由自定义硬件实现的第一级触发系统选择,然后由高级触发器中软件实现的算法进行选择[13]。第一级触发器以低于100 kHz的速率接受来自高达40 MHz束交叉的事件,该速率由高级触发器以约1 kHz的速率将事件记录到磁盘进一步降低。
在真实和模拟数据的重建和分析、探测器操作以及实验的触发和数据采集系统中,使用了广泛的软件套件[14]。
校准研究使用的数据是ATLAS在2015年至2018年pp碰撞中收集的,所有子探测器都在运行,对应的综合光度为140。在数据采集过程中质子束交叉间隔为25ns。Run 2数据的每个束交叉()的平均交互次数是34。在生成和重建模拟数据时,考虑了这些条件以及探测器配置和重建阈值的条件[15]。
基于蒙特卡罗(MC)的校准使用MC模拟的双射流和多射流事件。使用Pythia v8.230[16]作为模拟dijets的标称MC生成器。使用A14 tune[17]和nnpdf2.3 [18] parton分布函数(PDF)集模拟dijet事件的样本。重味强子的衰变用EvtGen建模[19]。
利用几个备选样本研究了MC模拟对校准的影响,并在此基础上确定了不确定度。使用Sherpa 2.2.5[20]生成器模拟了两种不同的dijet样本。首阶过程中包含矩阵元素计算,有序淋浴使用基于Catani-Seymour偶极子分解的默认Sherpaparton淋浴[21],使用CT 14nnlo PDF集[22]。这些样本中的第一个使用了基于簇碎片的专用SherpaAHADIC模型进行强子化[23]。第二个样本以相同的配置生成,但使用了Pythia 6[24]的Lund弦碎片模型及其衰变表的Sherpainterface。这两组样本被用来评估来自强子化模型的不确定性。
使用Herwig 7.1.6[25,26,27]对两组样本进行模拟,并使用NNPDF 2.3lo PDF集。这些样本包括在矩阵元素水平上的过程,以及使用基于Catani-Seymour减法方案[31,32]的分裂核的默认角有序部分子阵雨[28]或偶极部分子阵雨[29,30],在这两种情况下,都使用簇强子化。
采用与Pythia 8接口的Powheg Box v2[33,34]制作了NLO精度的多射流生产备选样品。这些都是在Powheg Box v2中实现的dijet过程中生成的[35]。将底层Born构型的值作为重整化和分解尺度,使用nnpdf3.0 nlo [36] PDF。pythiaa14曲调和NNPDF 2.3lo PDF用于淋浴和多部分交互。这些样本包括矩阵元素中不同扰动尺度下的每事件权重变化,不同的部子分布函数及其不确定性,以及Pythiaperturbative shower的不确定性。该多射流样品被用作原位互校准的标称MC样品,而Powheg Box v2[33,34]与Herwig[27]通过角有序parton淋浴[28]和NNPDF 2.3lo PDF作为备选样品。
对于原位射流分析,使用NNPDF 3.0nnlo PDF集[20]和调谐参数的AZNLO集[38],使用MadGraph + Pythia8[37]生成具有射流(Z+射流)的Z玻色子样品。使用Sherpa 2.2.11作为备选MC样本。标称射流样本是用Pythia v8.230[16]使用A14调优参数集[17]和NNPDF 2.3 PDF集生成的。分别制备了直接光子组分和碎片光子组分的+射流样品。在+jet事件中使用的备选样本是Sherpa 2.2.2和NNPDF 3.0nnlo PDF集[20]。
所有样本都使用全检测器模拟和使用Pythia8模拟的叠加最小偏差相互作用进行重建,这些相互作用具有调整参数的A3集[39]和NNPDF 2.3lo PDF集,以表示在相同或附近的束交叉(堆积)期间的多个pp相互作用。在数据分析期间,对模拟中堆积相互作用的平均数量的分布进行了重新加权,以匹配Run 2数据中的观察结果。
这些研究中的射流是用FastJet软件包中实现的带有半径参数的反算法重建的[40]。四动量物体被用作算法的输入,可以是MC的发生器级粒子,带电粒子轨迹,量热计能量沉积,或后两者的算法组合,如在粒子流(PFlow)重建技术的情况下。MC生成器级别的粒子称为真值粒子。重建射流使用PFlow对象(pfo)作为射流重建的输入,pfo将跟踪器和量热计的测量结果结合起来,形成射流重建的输入信号。具体来说,由带电粒子沉积在量热计中的能量从观察到的拓扑簇中减去,并由与这些拓扑簇匹配的轨迹动量取代,如文献[3]所述,并在文献[4]中进行了更新。与仅使用量热计信息重建的射流相比,由此产生的PFlow射流具有更高的能量和角分辨率、重建效率和堆积稳定性。
带电粒子轨迹用于PFlow重建和导出校准。这些轨道是在内部检测器完全接受的情况下重建的,除非另有说明,否则必须具有一个,并且必须满足基于ID子检测器中命中次数的标准。此外,轨迹必须满足mm,其中为轨迹最接近硬散射主顶点沿z轴的距离。校准中使用的轨迹与使用鬼关联的射流相匹配,该过程在射流重建期间将它们视为无限性的四向量,并将它们分配给与它们聚集在一起的射流[41]。
发生器级喷流,称为真值喷流,使用稳定的终态粒子(定义为具有mm的粒子)重建,不包括介子、中微子和堆积相互作用中的粒子。发生器级射流用和选择,用于MC校准的重构射流用和选择。
摘要
1 介绍
2 ATLAS探测器
3.数据样本和模拟事件
4 的simulation-based校准
5 原位分析
6 结论
笔记
参考文献
致谢
作者信息
搜索
导航
#####
本节详细介绍了基于模拟的射流能量刻度校准,将平均射流能量恢复为真值射流能量。这些步骤的事件选择在4.1节中描述,校准分四个步骤完成。前两个步骤应用堆积修正来消除由于在相同(及时)或附近(超时)束交叉中额外的pp相互作用而产生的过量。第4.2节中描述的第一种堆积校正基于事件和射流区域测量的中位数密度(“堆积密度校正”)进行减法[41,42],将模拟中使用的堆积模型的灵敏度降至最低。接下来,基于使用模拟样本导出的校正,应用对事件()中重构初级顶点数量的残差依赖的校正(“残差堆积校正”),如第4.3节所述。第三步,在4.4节中详细介绍的绝对JES校准,校正射流,使它们在能量和方向上平均与dijet MC事件的真射流一致。最后,如第4.5节所述,通过减少重建射流响应对使用跟踪、量热计和介子室探测器系统信息构建的观测值的依赖,全局校准提高了射流分辨率和相关不确定性。
基于模拟的射流能量刻度校准的所有阶段都使用相同的事件选择。通过对PFlow射流与真值射流的比较,采用MC模拟确定了射流的能量尺度和分辨率。要求真值射流和重构射流满足完全包含在检测器接受范围内,另外还要求真值射流具有。未经校准的射流具有正能量,但在应用第4.2-4.3节中描述的校正后,其能量可能变为负能量。在确定低能时平均射流能量响应()时,通过要求重构射流具有4.2节所述的堆积密度校正后,但不要求具有4.3节所述的校正后,减少了偏差。
事件需要至少有一个重构的主顶点,其中至少有两个匹配的轨迹。在模拟重构事件中,主顶点是轨迹动量平方和最大的重构主顶点,而在真值层面,主顶点对应的是模拟硬散射过程的主顶点,而不是动量传递最高的碰撞。这导致在某些事件中,堆积碰撞比硬散射碰撞具有更大的动量传递。对于MC样本,要求重建点和真值初级点的z坐标位置在0.2 mm以内。事件要求至少有两个重建喷气机,和至少一个真实喷气机。使用角距离与要求的真值射流在几何上匹配PFlow射流。此外,真值射流需要与所有其他真值射流隔离,而重构射流需要与所有重构射流隔离。为了减少堆积碰撞的动量传递比硬散射碰撞大的事件的贡献,要求两个领先的重建射流的平均值不大于。
堆积相互作用改变了射流的能量尺度,并且在相同或附近的束交叉处额外的pp相互作用会影响射流的重建。射流校准的第一阶段被称为“堆积密度校正”,根据射流的面积和事件中的中位数密度减去堆积的预期贡献[41]。为了计算射流面积A,一个密集的,均匀分布的无限小的软鬼粒子被覆盖在事件的顶部。然后,定义A为聚类后与给定射流匹配的所有鬼成分的四动量之和的横向动量,经鬼成分横向动量密度归一化。
每个事件的中位数堆积密度由采用算法[43,44]聚类的所有射流的中位数密度()估算,半径参数为0.4:
索引I在喷流上枚举。在这个计算中,只使用了喷流,因为在这个区域之外,由于物理和探测器效应的结合,喷流急剧下降。
假设堆积是均匀扩散的背景,堆积对射流能量的贡献可以用射流面积乘以中位数密度的乘积来近似表示。堆积密度校正后的射流定义为
与未校正射流的比值作为射流四动量的比例因子,因此不影响其方向。
以前,计算的输入与用于构建射流的输入相同:中性PFlow对象和满足mm的带电PFlow对象[4]。然而,这会导致包含硬散射轨迹的偏差,将中位数密度转移到更高的值,特别是当硬散射过程具有大的射流多重性时。为了防止这种偏差,研究了“堆积边带”(PUSB)定义,它使用中性PFlow对象和满足mm的带电PFlow对象作为输入。使用边带切割的堆积总量预计与标称标准相似,因为类似数量的堆积将满足这些标准。这确保了带电堆积组件的事件间相关性的最小损失,而带电强子减法切割不会将其去除。
如第5节所述,在特定的事件选择中测量JES,但这些校准适用于许多最终状态。需要一个不确定性来掩盖在模拟不同事件拓扑中偏倚之间的差异时所使用的模型的潜在不足,特别是dijet事件和jet事件之间偏倚之间的差异。射流事件在几个方面与dijet事件不同,包括夸克-胶子组成、颜色流动和过程的动量转移,这使得它成为一个很好的拓扑结构,可以用来估计潜在偏差的大小。通过比较数据样本在两种不同事件拓扑中的值之间的差异来估计给定的偏差,以衡量数据MC模拟中使用的模型的潜在不足:
传播到射流能量尺度不确定度的偏差为数据样本在平均值处确定的偏差:
射流选择使用最低的无预标单μ子触发器,需要两个μ子带、、和,而dijet选择使用最低的无预标单射流触发器,需要一个带、、和大于带电粒子流物体携带动量5%的先导射流。
图1显示了两个过程中作为数据和模拟的函数的依赖关系,比较了上面描述的两个定义。下面的面板比较了两个过程中的值。图中显示了两种不同的Sherpadijet样本:先前校准[4]时使用的2.1.1样本[45]和现在使用的2.2.5样本,而对于喷气机,只使用Sherpa2.2.1。夏尔巴人2.2。X个样本包括对多部子相互作用(MPI)模型的改进,该模型直接影响中的偏差。dijet Sherpa 2.1.1样品与喷流Sherpa 2.2.1样品之间的差异明显大于喷流Sherpa 2.2.5样品与喷流Sherpa 2.2.1样品之间的差异,之前使用具有不同MPI模型的dijet Sherpa 2.1.1样品和喷流Sherpa 2.2.1样品确定偏差。使用更新的dijet Sherpasample,使用一致的MPI模型和射流,结果偏差减少了四倍,显示了MPI建模在MC模拟中的重要性。新的定义使不同拓扑之间的差异显著减小,并且通过仿真可以更好地描述数据。同样,对定义的改进几乎导致了不确定性的三倍改进,这可以从两种不同定义的data和sherpa2之间的差异中看出。总之,这些改进将JES模型的不确定性降低了近7倍。
图1
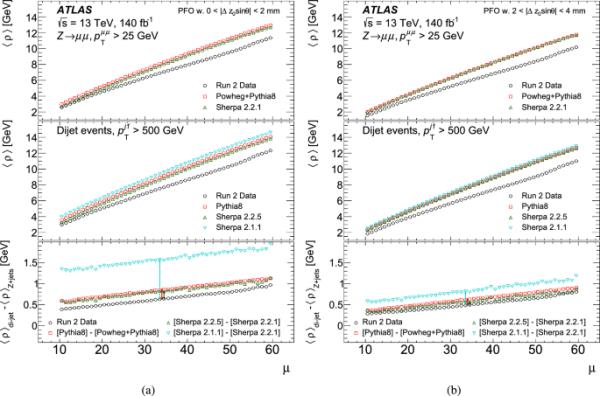
对于data、Pythia8、Sherpa 2.2.5和Sherpa 2.1.1的(顶部)+喷射和(中间)喷射选择,作为函数的分布。下面的面板显示了两种拓扑之间的差异,用于确定跨拓扑的外推的不确定性,由垂直箭头表示。左图显示了由射流成分构建的:中性PFOs和带mm的带电PFOs,右图显示了使用满足新边带选择的中性PFOs和带电PFOs构建的
为了进一步减小堆积的影响,基于,,重构射流(),重构射流(),对残余堆积进行校正。由于用于重建轨道以寻找主要顶点的硅跟踪探测器的快速响应,它对实时堆积敏感,而对超时堆积敏感,因为它占给定束交叉周围堆积的平均数量。通常情况下,及时堆积会增加喷气机的能量,而超时堆积会降低喷气机的能量。射流能量尺度对超时堆积的负依赖是由于液-氩量热计的脉冲形状,在记录信号后不久的一段时间内,脉冲形状为负[46]。对剩余堆积校正的两种方法进行了比较。
4.3.1 1D残余堆积修正
第一种策略,被称为“1D残余堆积校准”,遵循参考文献[4]中概述的方法,其中根据事件的和应用额外的校正
其中和确定如下。为了确定,首先,用在,和的箱子中的直线拟合对的依赖性。这个函数的斜率作为每个桶的依赖关系。这些斜率的平均值被认为是对给定和bin的依赖。对于每个箱,平均依赖关系拟合为的函数与的对数函数。在25处的对数拟合值作为标称校正,因为堆积效应与低喷流最相关。最后,在每箱值上拟合分段线性函数,减少统计波动并在整个范围内提供连续修正。为了确定,同样的过程是重复的和切换的,以获得依赖。
4.3.2 3D残余堆积校正
一维残余堆积校正不考虑和之间的相关性,也不考虑堆积贡献作为射流函数的变化。3D残余堆积校正的设计就是为了包含这些相关性。在此校准中,射流尺度作为(,,)的函数平移以匹配真射流尺度,同时校正堆积效应和检测器效应。作为计算由。给出的修正量的参考。对于和的极值,如果没有足够的事件来确定准确的校正,则使用最接近的非空(,)bin(具有相同的)来确定校正,并对结果进行平滑处理。该平均差值拟合为使用线性加对数函数的函数,在,和的容器中,使用带有的射流确定。修正后的值由
通过构造,该剩余堆积校准将堆积校正与探测器效应校正结合起来,将射流能量尺度校正为真射流尺度。这与1D残余堆积校正形成对比,该校正旨在专门消除堆积对射流规模的影响。研究了几种只校正堆积的选项,但发现这些选项要么增加堆积依赖性,要么导致有问题的影响,如大部分带负的射流。
4.3.3 不同剩余堆积修正量的比较
图2显示了剩余堆积修正的不同选项的比较。如图所示,残余堆积校准对于改善具有的射流的堆积依赖性特别有用。总体而言,对于一维残余堆积校正,高喷流对堆积的绝对依赖性增加,但对响应的相对影响较小。虽然1D残余堆积校正在其优化范围(20-30)内表现最佳,但它在其他射流上具有相当大的堆积依赖性。此外,由于1D残余堆积校正针对同一bin进行了优化,因此其性能似乎通过构建而增强,而更差的bin将显示更差的性能。三维残余堆积校正显着降低了校准的堆积依赖性,特别是在高。基于这些结果,剩余的报告研究使用了3D剩余堆积校准。
图2
(左)和(右)在不同的残余堆积修正后的依赖关系。圆圈表示一维剩余堆积改正量,正方形表示三维剩余堆积改正量。这显示了(上),(下)的喷气机
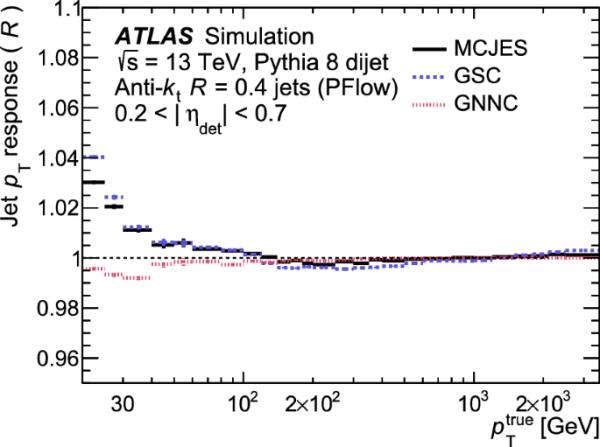
绝对射流能量标度(MCJES)和校正提供了能量和作为和的函数的校准函数,使得射流与真实射流能量和的平均值一致。由于量热计测量的是粒子的能量,而不是横向动量,所以这个修正是由射流能量的函数决定的。射流能量响应,定义为与高斯函数对分布核心的拟合的平均值,在和箱中测量,其中是从探测器几何中心指向的射流,用于消除关于探测器哪个区域正在测量射流的任何歧义。与期望值1的差称为非闭包,在不确定性范围内具有期望值的区域称为闭包。
应用残差校准后的射流能量响应如图3所示为与的函数。这与之前ATLAS实验的JES校准不同,因为射流能量响应已经接近于单位,这意味着校正相对较小。这是3D残余堆积校正的一个特征,它将射流的能量尺度移至接近真实尺度,尽管与高位存在一些显着差异,其中残余校准不足以捕获能量响应的行为。由于3D残余堆积校正中的项是使用射流确定的,因此射流能量响应在能量对应于时从1移开。
图3
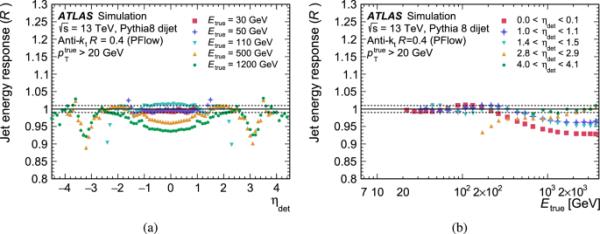
MCJES标定前的射流能量响应a为固定能量的函数,b为真射流能量的函数。a方形表示对的响应,加号表示对的响应,下三角形表示对的响应,上三角形表示对的响应,圆圈表示对的响应。b正方形表示对的响应,加号表示对的响应,下三角形表示对的响应,上三角形表示对的响应,圆圈表示对的响应
直接预测射流能量响应取决于用于导出校准的分布。总体而言,对于给定的响应分布近似为高斯分布,但对于给定的响应分布不是高斯分布[47]。因此,校准采用数值反演技术[5],其中,对于每个仓,将射流能量响应拟合为的函数,并利用该函数的反函数确定作为的函数的射流校准因子。下面比较了确定拟合函数的两种方法,即N阶多项式拟合和惩罚样条。
4.4.1 多项式适合
按照参考文献[4]中概述的步骤,多项式拟合被定义为的函数,其中为拟合多项式的最大阶。在给定的拟合函数中,使用Pearson检验确定最佳拟合函数[48]。校准因子通常冻结在3和之间的依赖能量,以减少统计波动,而在为时,对校准因子进行线性外推。
10/24/11惩罚样条函数
在多项式拟合函数的基础上,研究了惩罚样条的拟合方法。N次的样条S(x)是N次的分段多项式函数,其中样条的片段在称为结点的点相交,并且一阶导数在结点上连续。样条可以由b样条基函数定义[49]
其中n为数据拟合点的个数,为对各个基函数进行加权的控制点,t为结点。因为对于结点定义的范围之外的x,使用基于样条的低(高)末端的前(最后)五个点的线性外推来添加低(高)能量值的外推。
样条将过拟合数据,因为基函数需要精确地通过结点,在这种情况下,结点对应于确定响应的能量。对于一组点和它们对应的值,这可以通过使用惩罚b样条(P样条)来缓解,其中包括一个额外的平滑惩罚项P,最小化
其中a和b对应于惩罚项所包含的范围,与,惩罚参数被选择并固定。在这些研究中,x值对应于,y值对应于射流能量响应。随着从0到的增加,结果从样条回归到线性回归,并且该参数能够在曲率惩罚和与数据的密切拟合之间折衷。每个bin的惩罚参数动态定义为
其中i遍历n个数据拟合点,为调节参数,为定义为的点权重,其中为从迭代拟合到高斯函数的响应拟合不确定性。
对于这些研究,使用Splinter框架[50]实现样条,并使用三度样条,经验设置为0.1。为了检查过拟合,对统计独立事件进行校准和闭合检验。
4.4.3 校正比较
不同能量值下MCJES闭包拟合技术的比较如图4所示。这两种方法在高能量时都能提供1%的闭合,而在低能时,p样条方法比多项式拟合提供更好的闭合。总体而言,p样条校正在所考虑的范围内提供1%以内的封闭,除了由于快速变化的响应和能量响应中的非高斯项而使校准变得困难的少数箱。其余的研究使用由p样条拟合确定的校正,因为它提供了最佳的整体闭合。
图4
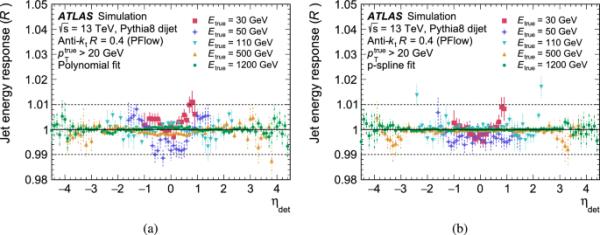
固定能量下的射流响应在多项式MCJES校准步骤后是a的函数,在p样条MCJES校准后是b的函数。方号表示对…的响应,加号表示对…的响应,向下的三角形表示对…的响应,向上的三角形表示对…的响应,圆圈表示对…的响应
4.4.4 绝对MC射流校准
除了射流能量外,采用与JES校准类似的方法校准射流伪快度,以纠正重建中的偏差,遵循参考文献[4]中的策略。这种偏差在量热计不同部分之间的过渡区域最为明显,在那里,不同探测器的不同响应人为地改变了射流一侧的重构能量,改变了重构能量。在桶-endcap()和前-endcap()转换中特别需要这些更正。偏差定义为,由对高斯函数的迭代拟合确定,并在逐喷的基础上通过。这种修正只适用于射流的和,并作为和的函数参数化。对于这种校正,只研究多项式拟合,最多使用一个三阶多项式。in和E的改正量之间有很小的相关性,所以这个改正量是与JES同时导出的。
绝对MCJES校准基于射流的E和修正射流能量响应。然而,还有许多其他因素有助于射流响应,包括射流中的能量分布,能量沉积在不同量热计层上的分布,以及射流中产生的强子类型。许多这些特征取决于喷流是由夸克还是胶子引发的。这可以在图5中看到,它显示了具有不同初始部分的射流的射流响应分布的示例,以及射流响应作为的函数,其中部分标签由与真值射流相关的最高能量部分鬼定义。不仅不同的喷气味道(即初始部分的味道)存在差异,而且行为也随着喷气的变化而变化。夸克发起的喷流往往有更少的强子,每个强子都有更高的喷流比例,这通常会导致对热量计的进一步贡献。相比之下,胶子引发的喷流通常有更多、更低的强子,导致较低的量热计响应和更宽的横向轮廓。这些行为由于粒子流重建的使用而变得更加复杂,这进一步增加了对射流中带电粒子的依赖。
射流响应也受到MC模型的影响,如图6所示的射流响应差异可以看出。总的来说,大多数MC预测对夸克发起的喷流具有相似的行为,而胶子发起的喷流之间的差异可能相当大。这是由于MC生成器对软辐射量的预测与其在射流中的拓扑分布之间存在差异。与其他模型相比,隆德弦模型在强子化模型的行为上有一些分离,隆德弦模型倾向于预测更高的胶子响应,而喷流的差异更大。这主要归因于重子和介子携带的射流能量的比例[51]。
全球喷流特性校准应用基于喷流个体特性的进一步校正。虽然这些校正对校准的整体关闭影响很小,但不同类别的射流的关闭显着改善,从而提高了JER。此外,这种校准减少了JES MC预测之间的差异,从而降低了建模的不确定性。下面概述了两种获得全局定标的方法:一种是在之前的工作[4]中描述的全局顺序定标(GSC),另一种是一种新的方法,即全局神经网络定标(GNNC)。这两种修正都是在对应于不同探测器区域的桶中导出的,在统计不确定性和结果的普遍性之间建立了平衡。
图5
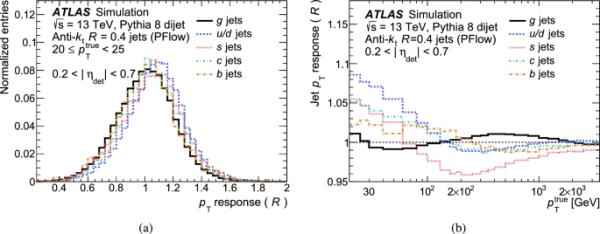
a不同喷流口味的喷流响应分布,b几种不同喷流口味的喷流响应作为的函数。实线表示胶子喷流的响应,长虚线表示轻夸克喷流的响应,短虚线表示奇异喷流,中短虚线交替表示粲喷流,长短虚线交替表示底喷流
图6
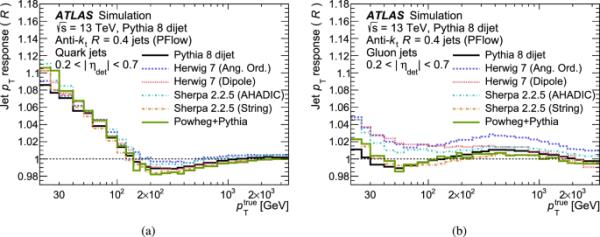
对于夸克喷流和胶子喷流的几个不同的MC预测,喷流响应作为函数。实线表示Pythia8,长虚线表示herwiga有角度有序的parton阵雨,短虚线表示herwiga有偶极子阵雨,中短虚线交替表示Sherpa与AHADIC强子化模型,长短虚线交替表示Sherpa与弦强子化模型,长虚线与三个短虚线表示Powheg+Pythia
4.5.1 全局序贯校准
GSC是一系列乘法修正,用于解释量热计对不同类型射流响应之间的差异,从而在不改变射流能量响应的情况下提高射流分辨率。GSC是基于全球喷流观测数据,如量热计中能量沉积的纵向剖面、与喷流匹配的跟踪信息,以及与喷流后面的介子室活动相关的信息。六个改善JER和减少建模不确定性的可观测值被用作GSC的输入。每个GSC修正射流四动量推导和应用独立和顺序,使用以下程序。首先,对于给定的GSC观测值,使用与MCJES校准相同的程序,射流响应分布适合于每个桶,和GSC观测值。接下来,将这些拟合值除以给定容器中响应的包含值,以避免改变射流校准的尺度。然后,对于GSC可观测的每个bin,在给定的(,)bin中进行线性平滑后,执行射流响应的数值反演。然后,对给定bin的结果响应同时进行平滑处理,并使用高斯核对GSC进行观察。因为GSC是按顺序应用的,所以有可能以系统的方式验证每个GSC更正,使用数据测试输入变量的任何错误建模的影响。这样的研究是为了验证顺序校正程序。
GSC的六个阶段,按照应用的先后顺序是
:带电粒子携带的射流的比例,通过与幽灵相关的轨迹测量,
:强子瓦量热计第一层测得的射流能量占比(),;
:被测在第三层的电磁LAr量热计,;
:与喷气机有关的幽灵音轨的数量,
:也称为轨迹宽度,是喷流轴与所有与喷流相关的幽灵轨迹之间的平均加权横向距离。
:与幽灵射流相关的μ子轨道段的数量;
这种校正,也称为穿孔式校正,减少了由于高喷流未完全包含在量热计中而引起的响应分布的尾部。与其他校正不同的是,校正是作为射流能量的函数而不是射流的函数来应用的,因为这种效应与逃离量热计的能量有更强的相关性。
在MC模拟中,PFlow射流在每次GSC修正后的射流响应如图7所示。在低能量下,射流能量尺度在1%以内,而在代替能量确定响应时,引入了少量的非闭合性。表示的分数射流分辨率用于确定射流能量重构中波动的大小,其中为射流响应分布与高斯函数的拟合宽度除以拟合的平均值。图7显示了在MC模拟中PFlow射流的情况。随着更多校正的应用,分数射流分辨率提高,射流响应对射流风味的依赖减少,因为具有不同特征的射流的校准得到了改进。和的影响在图7中最为明显,但不同校正的相对影响随函数而变化。此外,这些修正减少了在包容性情况下不太明显的影响。例如,穿透修正与能量有关,因此它主要影响对高能射流敏感的分析,但其影响在包容性分布中并不明显。
图7
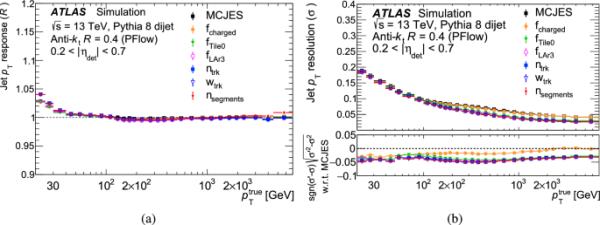
a GSC各阶段校准后的射流响应,b MCJES、校正后、校正后、校正后、校正后、校正后、校正后、校正后和校正后的射流分辨率
4.5.2 全局神经网络标定
GSC仅限于使用相对不相关的变量进行校正,因为否则,由于可观测值之间的相关性,每个顺序步骤可能会干扰先前的校正。这个约束是该方法的基础,限制了可能应用的校正集。然而,当增加额外的观测值并考虑其相关性时,同时校准更为合适[52]。作为顺序校准的替代方案,深度神经网络(DNN)被训练以确定基于各种射流特性的同步校正,从而能够使用相关变量来确定全局射流特性校正。由于分析是根据喷流做出选择的,DNN的设计是为了纠正喷流响应,而GSC则保持能量响应不变。
为了提高基于探测器几何形状的性能,对用于导出GSC的每个区域进行DNN训练,以基于各种射流和事件级特征对射流进行校正。dnn使用Keras[53],使用Adam[54]优化算法进行训练。该网络有三个具有swish激活函数的隐藏层[55]和一个具有线性激活的单节点输出层。节点数量针对每个bin进行了优化,范围在100到300之间。该网络使用泄漏高斯核(LGK)损失函数[56]
式中为射流响应,为相应的NN预测,和为可调参数。作为,LGK损失学习模式,第二项确保误差函数相对于当前权值的梯度在很大程度上不会消失。在响应不是完美高斯分布的情况下,学习模式的偏差较小,因此比学习分布均值的损失函数具有更好的封闭性。
网络架构的选择是基于结果的闭包进行超参数优化的结果,其中超参数是涉及网络结构的参数。训练是用批量大小的喷气机完成的,学习率为。对于LGK损失,参数选择为,并基于超参数扫描。训练是为了最小化LGK损失函数,并且继续训练直到五个epoch的损失没有改善。增加耐心对结果的质量没有明显的影响。使用未加权事件是因为这样可以避免由于事件权重之间的巨大差异而导致的训练问题。由于目标是响应,而不是射流本身,所以均匀的重量对最终结果没有太大的影响。在训练中只使用事件中的两个主要射流,因为事件是使用dijet过程模拟的,因此这避免了使用纯粹来自parton shower的射流的潜在偏差。对于每个bin,我们训练了几个网络,并选择具有最佳封闭性的网络作为最终结果。
考虑了几组变量作为神经网络的输入,训练中使用的最终变量列表如表1所示。此列表包括GSC校准中使用的所有变量,并添加了更多关于射流运动学的信息,更多关于不同量热计层中能量沉积的颗粒信息,以及堆积测量。虽然残差堆积校正消除了大部分堆积依赖,但绝对MCJES校准重新引入了一些依赖,因此和包含在训练中。某些区域不存在某些量热计层,在这种情况下,它们被设置为零。明确地从NN训练中使用的输入变量列表中删除这些可观察值对结果的影响可以忽略不计,因此所有区域的训练变量集保持相同。
表1作为GNNC输入的变量列表。带有*的变量对应于GSC也使用的变量
该校准的射流封闭度通常优于1%,但也有一些波动,有时可能略高于此值。这些波动的幅度随每次DNN训练而变化,但在不同的DNN超参数、损失函数和训练目标中持续存在。为了减轻这种情况,在GNNC之后推导了一个额外的校准,使用第4.4节中概述的p样条方法,但使用真值射流作为目标而不是能量。这是在宽度为0.1的容器中导出的,这比使用相同的容器作为GNNC校正提供了更好的性能。这对射流分辨率的影响可以忽略不计,只是为了提高校准的封闭性和平稳性。
4.5.3 方法比较
图8显示了一个代表性箱体在MCJES、GSC和GNNC之后的射流响应比较。按照设计,GSC不会改变喷气机的能量响应。由于JES校准将重建的能量尺度移动到与真值尺度相匹配的位置,这可能导致射流中存在一定的不闭性,这在低位尤为明显。GNNC的设计是为了改变射流的尺度以匹配真实射流,因此封闭在比GSC封闭更好。值得注意的是,虽然GSC可以以一种校正喷射尺度的方式应用,但这并不影响分辨率。其他箱子表现出类似的定性特征,尽管在MCJES和GSC之后的反应中看到的确切的不闭合略有不同。
图9显示了几个代表性箱子在MCJES、GSC和GNNC之后的射流分辨率的比较。在少数情况下,射流分辨率在最低的桶中变得更差,但这也是非闭合性最显著的地方,使得难以准确估计分辨率,特别是因为GNNC的规模不同于MCJES和GSC。由于MCJES和GSC的尺度大于1且斜率为负,因此在这些箱中测量的分辨率被略微低估[47],而GNNC的分辨率被正确估计,因为响应关闭。与GSC相比,GNNC的射流分辨率平均提高了15%以上,最大提高了25%以上。其他箱子显示出类似的15-25%左右的平均改进,最大改进通常超过30%,并且改进通常在更高的地方变得更加明显,其中分辨率改进是显著的,主要是由于额外检测器信息的改进。将GNNC性能与仅将GSC观测值作为输入进行比较的研究发现,GNNC的性能与GSC相似,这表明GNNC与GSC相比分辨率的提高是由于包含了额外的观测值。这是通过同时校正可观测值之间的相关性而实现的。GNNC比GSC提供了更大的射流能量分辨率改进,因此在本文的其余部分中使用了GNNC。
图8

喷气机关闭。实线表示MCJES,长虚线表示GSC,短虚线表示GNNC
图9
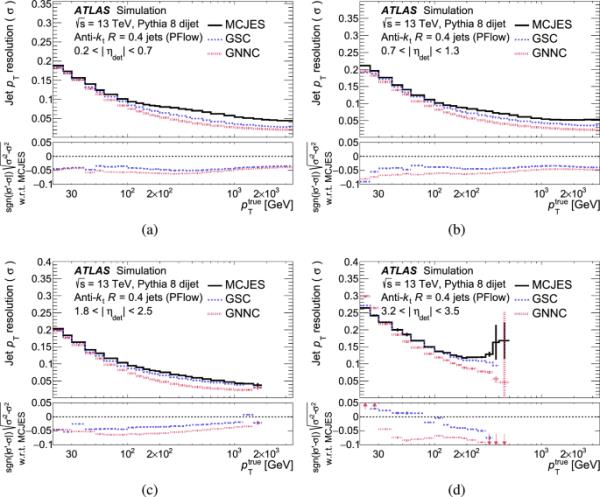
a、b、c和(d)的射流分辨率。实线表示MCJES,长虚线表示GSC,短虚线表示GNNC
4.5.4 味道不确定性
JES中的两种风味依赖不确定性来源于模拟,并解释了相对风味分数和对夸克和胶子引发的射流的不同反应。风味响应的不确定性解释了这样一个事实,即与夸克发起的射流响应不同,胶子发起的射流响应在发生器之间存在显着差异。这种不确定性定义为
式中为胶子启动射流的比例,和分别为Pythia8和herwig2中胶子启动射流的响应。味道成分的不确定性解释了夸克和胶子引发的射流响应不同的事实。这是根据胶子引发喷流的比例确定的,其中和是在Pythia8中测量到的夸克和胶子喷流响应,是样品中的不确定度,不确定度定义为
图10显示了MCJES、GNNC和GSC的风味成分和风味响应不确定性的比较。在MCJES校准后,对于超过100的射流变为负值,这表现为风味成分不确定度的下降。GSC和GNNC都可以减少这些不确定性,GNNC提供了更大的减少。对于每个桶,与GSC相比,GNNC在风味响应不确定性范围内平均提高了约15-25%,在风味成分不确定性方面提高了高达25%。
图10
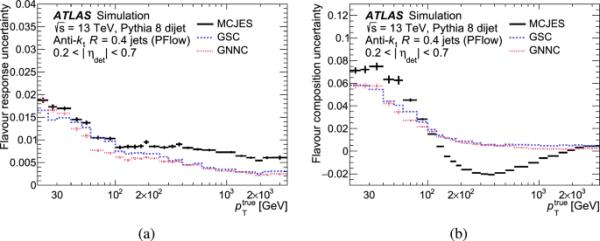
a香味响应的不确定度,b香味成分的不确定度。实线表示MCJES,长虚线表示GSC,短虚线表示GNNC
下载原文档:https://link.springer.com/content/pdf/10.1140/epjcs10052-023-11837-9.pdf



